زمان اجرای الگوریتم ضرب دو ماتریس

ضرب دو ماتریس، از بدیهی‌ترین و اساسی‌ترین الگوریتم‌هایی است که برای محاسبات عددی به آن نیاز داریم.

در الگوریتم بدیهی برای ضرب دو ماتریس A و B، برای محاسبه هر درایه از ماتریس لازم است که n عدد ضرب انجام شود. در نتیجه زمان اجرای الگوریتم [latex]O(n^3)[/latex] خواهد بود.

امروز در کلاس ساختمان داده سر الگوریتم استراسن بحث شد. الگوریتمی که با آن می‌توان دو ماتریس n در n را در زمان سریع‌تر از [latex]O(n^3)[/latex]، یعنی در زمان [latex]O(n^{2.807})[/latex] محاسبه کرد.

سوالی که مطرح شد این بود که زمان اجرای سریع‌ترین الگوریتم برای محاسبه ضرب دو ماتریس چقدر است؟ پس از الگوریتم استراسن که در سال ۱۹۶۹ ارائه شده بود، الگوریتم دیگری با زمان اجرای [latex]O(n^{2.376})[/latex] در سال ۱۹۹۰ و الگوریتم سریع‌تری با زمان اجرای [latex]O(n^{2.3729})[/latex] در سال ۲۰۱۳ و الگوریتم دیگری با زمان اجرای [latex]O(n^{2.3728639})[/latex] در سال ۲۰۱۴ ارائه شد. نمودار زیر از ویکی‌پدیا توان n در زمان اجرای الگوریتم ضرب دو ماتریس را در طی زمان نشان می‌دهد.

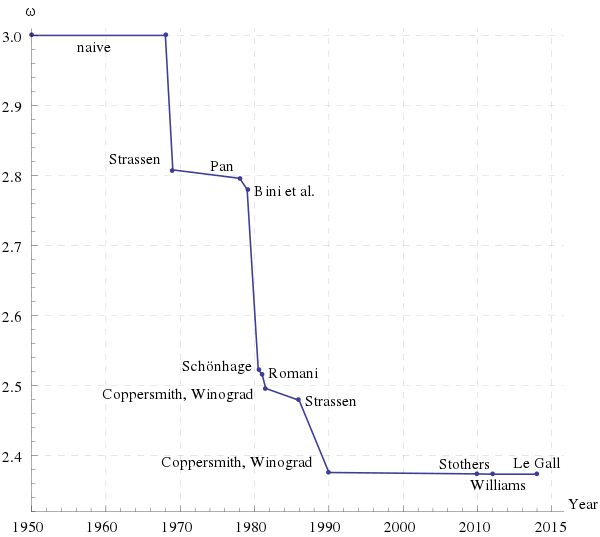
فرض کنید سریع‌ترین الگوریتمی که برای ضرب دو ماتریس وجود دارد زمان اجرایش حدودا [latex]O(n^{\omega})[/latex] است. سوال این است که این [latex]\omega[/latex] چند است؟ تا کنون می‌دانیم [latex]\omega\leq 2.3728639[/latex]. از طرفی چون باید جواب را تولید کنیم و ورودی را باید بخوانیم حداقل باید به اندازه خود ماتریس‌ها زمان صرف کنیم، پس [latex]2\leq\omega\leq 2.3728639[/latex]. اما بیش از این نمی‌دانیم. یعنی حتی نمی‌دانیم آیا [latex]\omega[/latex] از ۲ اکیدا بزرگ‌تر است یا خیر.

در هر صورت این مساله خیلی مساله جالبی است. و خیلی جالب است که پس از مدت‌ها هنوز نمی‌دانیم که آیا بیش از خواندن ماتریس‌های ورودی زمان لازم است برای تولید ضرب دو ماتریس و یا خیر. با این‌که مقدار [latex]\omega[/latex] را نمی‌دانیم، ولی می‌توانیم از این مقدار برای محاسبه زمان اجرای الگوریتم‌های دیگر استفاده کنیم. مثلا در مقاله‌ها می‌بینیم که زمان اجرای الگوریتم‌شان را بر حسب [latex]\omega[/latex] محاسبه کرده و گزارش می‌کنند.

منبع: صفحه انگلیسی ویکی‌پدیا در مورد ضرب ماتریس‌ها